Q.
Two identical small discs each of mass $m$ placed on a frictionless horizontal floor are connected with the help of a light spring of force constant $k$. The discs are also connected with two light rods each of length $2 \sqrt{2} \,m$ that are pivoted to a nail driven into the floor as shown in the figure by a top view of the situation. If period of small oscillations of the system is $2 \pi \sqrt{(m / k)}$, find relaxed length (in meters) of the spring.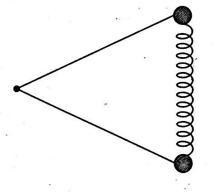
Oscillations
Solution:
