Question

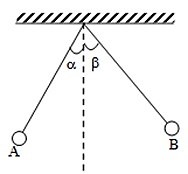
Two identical simple pendulums $A$ and $B$ are fixed at same point. They are displaced by very small angles $\alpha $ and $\beta \left(\beta > \alpha \right)$ respectively and released from rest. If collisions are elastic and length of strings is $l$ then find the time after which $B$ reaches its initial position for the first time

• A. $\pi \sqrt{\frac{l}{g}}$
• B. $2\pi \sqrt{\frac{l}{g}}$
• C. $\frac{\pi \beta }{\alpha }\sqrt{\frac{l}{g}}$
• D. $\frac{2 \pi \beta }{\alpha }\sqrt{\frac{l}{g}}$

Answer 1

Answer: (B)

Time period of both $A$ and $B$ .
$2\pi \sqrt{\frac{l}{g}}$
$A$ and $B$ collide after time $\frac{T}{4}$
After first collision, $B$ acquires amplitude of $A$ and second collision takes place after additional time of $\frac{T}{4}+\frac{T}{4}=\frac{T}{2}$ after second collision $B$ acquires its own amplitude and reaches its initial position after additional time of $\frac{T}{4}$
In this process time taken is $=\frac{T}{4}+\frac{T}{4}+\frac{T}{4}+\frac{T}{4}$
$\Rightarrow \, \, T=2\pi \sqrt{\frac{l}{g}}$