Q.
Two identical parallel plate capacitors, of capacitance $C$ each, have plates of area $A$, separated by a distance $d$. The space between the plates of the two capacitors, is filled with three dielectrics, of equal thickness and dielectric constants $K_1, K_2$ and $K_3$. The first capacitor is filled as shown in fig. $I$, and the second one is filled as shown in fig. $II$.
If these two modified capacitors are charged by the same potential $V$, the ratio of the energy stored in the two, would be ($E_1$ refers to capacitor (I) and $E_2$ to capacitor (II) :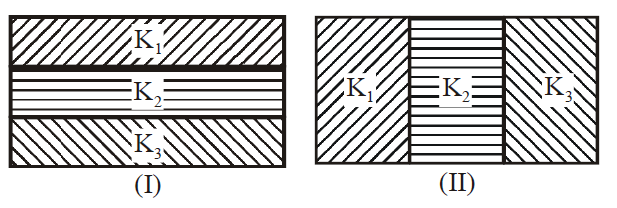
Solution:
