Q. Two identical conducting wires $AOB$ and $COD$ are placed at right angles to each other. The wire $AOB$ carries an electric current $I_{1}$ and $COD$ carries a current $I_{2}$ . The magnetic field on a point lying at a distance $d$ from $O$ , in a direction perpendicular to the plane of the wires $AOB$ and $COD,$ will be given by
NTA AbhyasNTA Abhyas 2022
Solution:
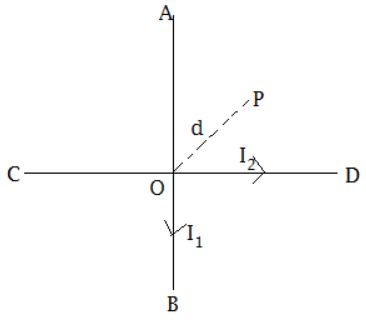
The magnetic field induction at a point $P_{1}$ at a distance $d$ from $O$ in a direction perpendicular to the plane of the wires and due to the currents through $AOB$ and $COD$ as shown, are perpendicular to each other and it is
Hence, $B= \, \sqrt{B_{1}^{2} + B_{2}^{2}}$
$\Rightarrow B=\left(\left[\left(\frac{\left(\mu \right)_{0}}{4 \pi } \, \frac{2 I_{1}}{d}\right)^{2} + \left(\frac{\left(\mu \right)_{0}}{4 \pi } \, \frac{2 I_{2}}{d}\right)^{2}\right]\right)^{\frac{1}{2}}$
$\therefore B=\frac{\left(\mu \right)_{0}}{2 \pi d} \, \sqrt{\left(I_{1}^{2} + I_{2}^{2}\right)}$

The magnetic field induction at a point $P_{1}$ at a distance $d$ from $O$ in a direction perpendicular to the plane of the wires and due to the currents through $AOB$ and $COD$ as shown, are perpendicular to each other and it is
Hence, $B= \, \sqrt{B_{1}^{2} + B_{2}^{2}}$
$\Rightarrow B=\left(\left[\left(\frac{\left(\mu \right)_{0}}{4 \pi } \, \frac{2 I_{1}}{d}\right)^{2} + \left(\frac{\left(\mu \right)_{0}}{4 \pi } \, \frac{2 I_{2}}{d}\right)^{2}\right]\right)^{\frac{1}{2}}$
$\therefore B=\frac{\left(\mu \right)_{0}}{2 \pi d} \, \sqrt{\left(I_{1}^{2} + I_{2}^{2}\right)}$