Q. Two identical charged spheres are suspended by strings of equal lengths. The strings make an angle of $30^{\circ}$ with each other. When suspended in a liquid of density $0.8\, g\, cm^{-3}$, the angle remains the same. If density of the material of the sphere is $1.6\, g\, cm^{-3}$, the dielectric constant of the liquid is
AIEEEAIEEE 2010Mechanical Properties of Fluids
Solution:
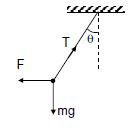
From fig,
$
\tan \theta= qE / mg
$
$
\tan 15^{\circ}=\frac{ kq ^2}{ d ^2 mg }
$
$\tan 15^{\circ}=\frac{ kq ^2}{1.6 V gd^{2 } } \ldots . .[ V$ is the volume $]$.
When system is suspended in liquid,
$
\begin{array}{l}
\tan 15^{\circ}=\frac{ kq ^2}{ K ( mg -\rho gg ) d ^2} \\
\tan 15^{\circ}=\frac{ kq ^2}{ K (1.6-0.8) Vgg^{2 } } \ldots \ldots .(2)
\end{array}
$
from (1) and (2) we get,
$
\frac{ kq ^2}{ K (1.6-0.8) V gd ^2}=\frac{ kq ^2}{1.6 V gd ^2}
$
$\therefore K =2=$ Dielectric constant of liquid.