Question

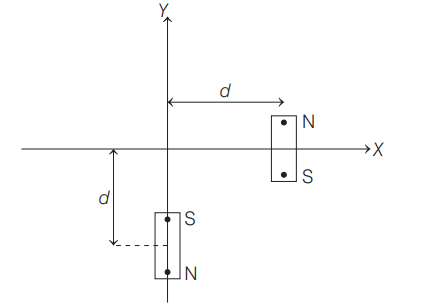
Two identical bar magnets of magnetic moment $M$ each, are placed along $X$ and $Y$ -axes, respectively at a distance $d$ from the origin (as shown in the figure). The origin lies on perpendicular bisector of magnet placed on $X$ - axis and on the magnetic axis of magnet placed on $Y$ - axis. If the magnitude of total magnetic field at the origin is $B=\alpha\left[\frac{\mu_{0}}{4 \pi} \frac{M}{d^{3}}\right]$, then the value of constant $\alpha$ will be $(d>>l$, where $l$ is the length of the bar magnets and direction of $N$ to $S$ in magnets is opposite with respect to each other)

• A. 2
• B. 1
• C. 3
• D. $\sqrt{5}$

Answer 1

Answer: (C)

Magnetic field due to axial magnet,
$B _{1}=\frac{\mu_{0}}{4 \pi} \frac{2 M}{d^{3}}$ (+Y direction)
Magnetic field due to equatorial magnet,
$B _{2}=\frac{\mu_{0}}{4 \pi} \frac{M}{d^{3}}$
$(+Y$ direction )
So, effective magnetic field
$B = B _{1}+ B _{2}=3 \frac{\mu_{0} M}{4 \pi d^{3}} $
$\Rightarrow \, \alpha=3$