Q.
Two identical balls $A$ and $B$ are released from the positions shown in the figure. They collide elastically on horizontal portion $MN$. The ratio of heights attained by $A$ and $B$ after collision will be (neglect friction)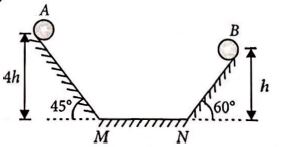
Work, Energy and Power
Solution:
