Q.
Two heavy right circular rollers of radii $R$ and $r$ respectively rest on a rough horizontal plane as shown in figure. The larger roller has a string wound around it to which a horizontal force $P$ can be applied as shown. Assuming that the coefficient of friction $\mu$ has the same value for all surfaces of contact and the smaller cylinder should neither roll nor slide. The minimum coefficient of friction so that the larger roller can be pulled over the smaller one is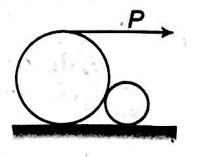
System of Particles and Rotational Motion
Solution:
