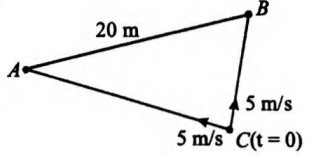
Q. Two fixed points $A$ and $B$ are $20$ metres apart. At time $t=0$, the distance between a third point $C$ and $A$ is $20$ meters and the distance between $C$ and $B$ is $10$ metres. The component of velocity of point $C$ along both $C A$ and $C B$ at any instant is $5 \,m / s$. Then the distance between $A$ and $C$ at the instant all the three points are collinear will be
Motion in a Straight Line
Solution:
The length of side $C A$ at any time $t$ is $=20-5\, t$.
The length of side $C B$ at any time $t$ is $=10-5 \, t$.
At the instant $A, B$ and $C$ are collinear
$(20-5\, t)+(10-5 t)=20$.
Solving we get $t=1$.
Therefore, length of $C A$ at $t=1$ is $20-5=15\, m$