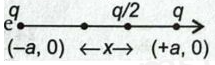
Question

Two equal point charges, $Q=+\sqrt{2} \mu C$ are placed at each of the two opposite corners of a square and equal point charges $q$ at each of the other two corners. The value of $q$, so that the resultant force on $Q$ is zero is

• A. $+0.5 \mu C$
• B. $-0.5 \mu C$
• C. $1 \mu C$
• D. $-1 \mu C$

Answer 1

Answer: (B)

From Coulomb's law, $F=\frac{1}{4 \pi \varepsilon_{0}} \frac{Q^{2}}{2 a^{2}}$
$F_{1}$ and $F_{2}$ will be directed as shown, for this both $q$ should be negative
$F_{1}=F_{2}=\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{Q q}{a^{2}}$
$F_{12}=\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{\sqrt{2} Q q}{a^{2}}$

For equilibrium of $Q$, we have
$F=-F_{12}$
$\frac{Q^{2}}{2 a^{2}}=-\frac{\sqrt{2} Q q}{a^{2}}$
$\Rightarrow q=\frac{Q}{2 \sqrt{2}}$
Given $Q=+\sqrt{2} \mu C$
$\therefore q=-\frac{\sqrt{2} \mu C}{2 \sqrt{2}}=-0.5\, \mu C$