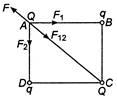
Q. Two equal point changes, $ Q=+\sqrt{2}\mu C $ are placed at each of the two opposite corners of a square and equal point charges q at each of the other two comers. The value of q, so that the resultant force on Q is zero is:
KEAMKEAM 2000
Solution:
From Coulombs law $ F=\frac{1}{4\pi {{\varepsilon }_{0}}}\,\frac{{{Q}^{2}}}{2{{a}^{2}}} $
$ {{F}_{1}} $ and $ {{F}_{2}} $ will be directed as shown, for this both q should be negative $ {{F}_{1}}={{F}_{2}}=\frac{1}{4\pi {{\varepsilon }_{0}}}.\frac{Qq}{{{a}^{2}}} $ $ {{F}_{12}}=\frac{1}{4\pi {{\varepsilon }_{0}}}.\frac{\sqrt{2}Qq}{{{a}^{2}}} $ For equilibrium of Q, we have $ F=-{{F}_{12}} $ $ \frac{{{Q}^{2}}}{2{{a}^{2}}}=\frac{\sqrt{2}Qq}{{{a}^{2}}} $ $ \Rightarrow $ $ q=\frac{Q}{2\sqrt{2}} $ Given, $ Q=+\sqrt{2}\mu C $ $ \therefore $ $ q=-\frac{\sqrt{2}\mu C}{2\sqrt{2}}=-0.5\,\mu C $