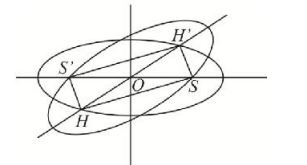
Question

Two concentric ellipses are such that the foci of each one are on the other and length of their major axes are equal. Let $e$ and $e^{\prime}$ be their eccentricities, then

• A. The quadrilateral formed by joining the foci of the two ellipses is a parallelogram
• B. The angle $\theta$ between their axes is given by $\theta=\cos ^{-1} \sqrt{\frac{1}{e^2}+\frac{1}{e^{\prime 2}}-\frac{1}{e^2 e^{\prime 2}}}$
• C. If $e^2+e^{\prime 2}=1$, then the angle between the axis of the two ellipses is $90^{\circ}$
• D. If $e+e^{\prime}=1$, then the angle between the axis of the two ellipses is $90^{\circ}$

Answer 1

Answer: (A), (B), (C)

Clearly $O$ is the maidpoint of $S S^{\prime}$ and $H H^{\prime}$
$\Rightarrow$ Diagonals of quadrilateral IISII 'S' bisect each other, so it is a parallelogram.
I.et $I I^{\prime} O I I=2 r \Rightarrow O I I=r=a e^{\prime}$
$H$ lics on $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ (supposc)
$\therefore \frac{r^2 \cos ^2 \theta}{a^2}+\frac{r^2 \sin ^2 \theta}{b^2}=1 $
$ e^{\prime 2} \cos ^2 \theta+\frac{e^{\prime 2} \sin ^2 0}{1-e^2}=1 \left[\because b^2=a^2\left(1-e^2\right)\right] $
$\Rightarrow e^{\prime 2} \cos ^2 \theta-\frac{e^{\prime 2} \cos ^2 0}{1-e^2}=1-\frac{e^{\prime 2}}{1-e^2} $
$\Rightarrow \cos ^2 \theta=\frac{1}{e^2}+\frac{1}{e^{\prime 2}}-\frac{1}{e^2 e^{\prime 2}} $
$\Rightarrow \theta=\cos \sqrt{\frac{1}{e^2}+\frac{1}{e^{\prime 2}}-\frac{1}{e^2 e^{\prime 2}}}$
For $\theta=90^{\circ}, \frac{e^2+e^{\prime 2}}{e^2 e^{\prime 2}}=\frac{1}{e^2 e^{\prime 2}} \Rightarrow e^2+e^{\prime 2}=1$