Q.
Two concentric circular loops, one of radius $R$ and the other of radius $2 R$, lie in the $x y$-plane with the origin as their common centre, as shown in the figure. The smaller loop carries current $I_{1}$ in the anti-clockwise direction and the larger loop carries current $I_{2}$ in the clock wise direction, with $I_{2}>2 I_{1}, \vec{B}(x, y)$ denotes the magnetic field at a point $(x, y)$ in the $x y$-plane. Which of the following statement (s) is ( are ) correct?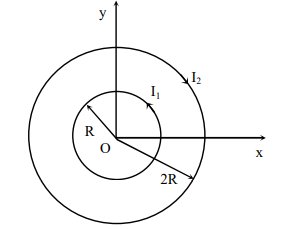
JEE AdvancedJEE Advanced 2021
Solution:

