Q.
Two coherent sources of sound, $S_{1}$ and $S_{2}$, produce sound waves of the same wavelength, $\lambda=1 m ,$ in phase. $S _{1}$ and $S _{2}$ are placed $1.5 m$ apart (see fig.) A listener, located at $L$, directly in front of $S _{2}$ finds that the intensity is at a minimum when he is $2 m$ away from $S _{2}$. The listener moves away from $S _{1},$ keeping his distance from $S _{2}$ fixed. The adjacent maximum of intensity is observed when the listener is at a distance $d$ from $S _{1}$. Then, $d$ is :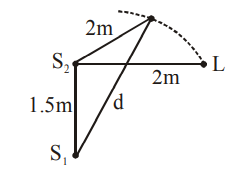
Solution:
