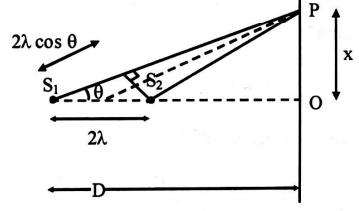
Q.
Two coherent narrow slits $S_{1}$ and $S_{2}$ emitting light of wavelength $\lambda$ in the same phase are placed parallel to each other at a small separation of $3 \lambda$. The light is collected on a screen $S$ which is placed at a distance $D(> > \lambda)$ from the slit $S_{1}$ and shown in figure. The distance $x$ such that the intensity at point $P$ is equal to the intensity at $O$ is $\frac{D}{2 \sqrt{5}} \times a$. Find the value of $a$.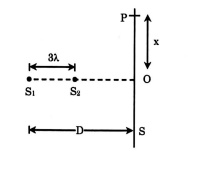
Wave Optics
Solution: