Question

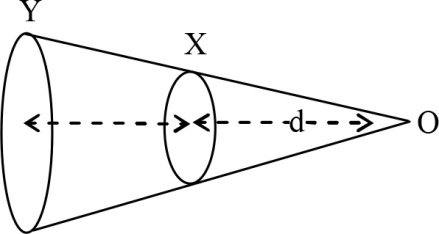
Two circular coils $X$ and $Y$ have the equal number of turns and carry equal currents in the same sense and subtend same solid angle at the point $O$ . If the smaller coil $X$ is midway between $O$ and $Y$ , then if we represent the magnetic induction due to bigger coil $Y$ at $O$ as $B_{Y}$ and that due to smaller coil $X$ at $O \, $ as $B_{x}$ , then :

• A. $\frac{B_{Y}}{B_{X}}=1$
• B. $\frac{B_{Y}}{B_{X}}=2$
• C. $\frac{B_{Y}}{B_{X}}=\frac{1}{2}$
• D. $\frac{B_{Y}}{B_{X}}=\frac{1}{4}$

Answer 1

Answer: (C)

[ For same angle $\alpha $ ]

$B=\frac{\left(\mu \right)_{0}}{4 \pi }\frac{2 M}{\left(\right. R^{2} + d^{2} \left.\right)^{\frac{3}{2}}}$
$ \propto \frac{R^{2}}{\left(\right. R^{2} + d^{2} \left.\right)^{\frac{3}{2}}}$
$\frac{B_{y}}{B_{x}}=\frac{\frac{R_{y}^{2}}{\left(\left[\right. R y^{2} + \left(\right. 2 d \left.\right)^{2} \left]\right.\right)^{\frac{3}{2}}}}{\frac{R_{x}^{2}}{\left(\left[\right. R_{x}^{2} + d^{2} \left]\right.\right)^{\frac{3}{2}}}}$
$R_{y}=2R_{x}$
$\Rightarrow \frac{B_{y}}{B_{x}} = \frac{1}{2}$