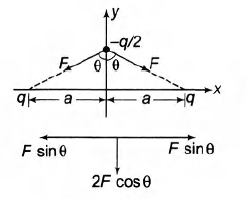
Q. Two charges, each equal to $q$, are kept at $x = - a$ and $x = a$ on the $x-axis$. A particle of mass m and charge $q_0=\frac{q}{2}$ is placed at the origin. If charge $q_0$ is given a small displacement $y ( y << a)$ along the y-axis, the net force acting on the particle is proportional to
Solution:
$F_{net} =2F \cos\, \theta$
$F_{net} =\frac{2kq\left(\frac{q}{2}\right)}{(\sqrt{y^2+a^2})^2}.\frac{y}{\sqrt{y^2+a^2}}$
$F_{net} =\frac{2kq\left(\frac{q}{2}\right)y}{(\sqrt{y^2+a^2})^{3/2}}$
$\Rightarrow \frac{kq^2y}{a^3} \propto y$