Question

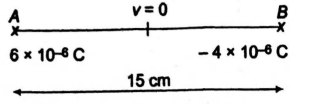
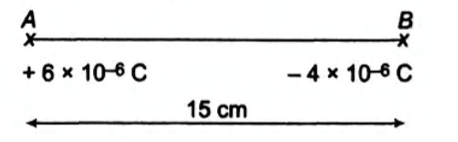
Two charges $ +6\, \mu C $ and $ - 4\, \mu C $ are placed apart as shown. At what distances from $A$ to its right, the electrostatic potential is zero (distances in cm)

• A. 4, 9 , and 60
• B. 9, 45, infinity
• C. 20, 45, infinity
• D. 9, 15, 45

Answer 1

Answer: (B)

$V_1 +V_2 = 0$
$\frac{Q_{1}}{4\pi \varepsilon_{0} r_{1}} + \frac{Q_{2}}{4\pi\varepsilon_{0}r_{2}} = 0 $
$ \frac{1}{4\pi\varepsilon_{0}}\left[\frac{6\times10^{-6}}{x} + \frac{-4\times 10^{-6}}{\left(15-x\right)}\right] = 0$
$ 9\times 10^{9} \left[\frac{6\times10^{-6}}{x} +\frac{\left(-4\times10^{-6}\right)}{\left(15-x\right)}\right] = 0 $
$\frac{ 6\times10^{-6}}{x} = \frac{4\times 10^{-6}}{\left(15-x\right)}$
$ 6\left(15 -x\right) = 4x$
$ 90 -6 x = 4x $
$10x = 90$
$ x = 9 \,cm$
Again at $45 \,cm$
Potential $V = \frac{6\times 10^{-6}}{45} + \frac{(-4\times 10^{-6})}{30}$
$ = 0.13 \times 6^{-6} - 0.13 \times 10^{-6}$
$ = 0$
At infinity
Potential $V =\frac{6\times10^{-6}}{\infty} +\frac{ 4\times 10^{-6}}{\infty} = 0$