Question

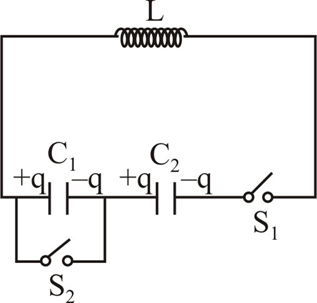
Two capacitors $C_{1}=C_{2}=\frac{1}{\pi ^{2}}\times 10^{- 2}F$ and inductor $L=2\times 10^{- 2}H$ are connected in series as
shown in the figure. Initially charge on each capacitors are $4\sqrt{3}\mu C.$ At $t=0$ switch $S_{1}$ is
closed and at $t=\frac{1}{400}$ sec, switch $S_{2}$ is also closed. The maximum charge on capacitor $C_{2}$
during LC oscillation is $k\sqrt{2}\mu C$ . Find $k$ .

Answer 1

Initial total energy is
$U_{i n i t i a l}=\frac{q^{2}}{2 C_{e q}}=\frac{2 q^{2}}{2 C}=\frac{q^{2}}{C}=\frac{\left(4 \sqrt{3}\right)^{2}}{\frac{1}{\left(\pi \right)^{2}} \times \left(10\right)^{- 2}}=4.8\times \left(10\right)^{4}$
Let's calculate angular frequency in first case when both capacitors are in series $\omega =\frac{1}{\sqrt{L C_{e q}}}\omega =\frac{1}{\sqrt{2 \times 10^{- 2} \times \frac{10^{- 2}}{2 \pi ^{2}}}}\omega =100\pi T=\frac{2 \pi }{\omega }=\frac{2 \pi }{100 \pi }\Rightarrow T=\frac{1}{50}sec$
At $t=\frac{T}{4}=\frac{1}{200}sec$ All energy will be stored in inductor .and $C_{1}$ is short-circuited
Maximum energy that can be stored in $C_{2}$ After that will be
$\frac{q^{2}}{2 C}=4.4\times 10^{4}q=\sqrt{4 . 4 \times 10^{4} \times 2 \times \frac{1}{\pi ^{2}} \times 10^{- 2}}=6.63\sqrt{2}$ 4