Q.
Two capacitors $C_{1}$ and $C_{2}$ in a circuit are joined as shown in the figure. The potentials of points $A$ and $B$ are $V_{1}$ and $V_{2}$ respectively. Then the potential of point $D$ will be
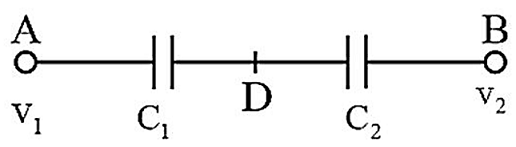
NTA AbhyasNTA Abhyas 2022
Solution:
Let the potential at point $D$ be $V$ and suppose that $V_{2}>V_{1}$ .
Then the potential drop across $C_{1}$ is $\left(\right. V - V_{1} \left.\right)$ and $C_{2}$ is $\left(\right. V_{2} - V \left.\right)$ .
Charge stored on the capacitor of capacitance $C_{1}$ is
$q_{1}=C_{1}\left(\right. V - V_{1} \left.\right)$
Charge stored on the capacitor of capacitance $C_{2}$ is
$q_{2}=C_{2}\left(\right. V_{2} - V \left.\right)$
As $q_{1} = q_{2}$ [capacitors are in series]
$\therefore C_{1} \left(\right. V - V_{1} \left.\right) = C_{2} \left(\right. V_{2} - V \left.\right)$
$\Rightarrow V=\frac{C_{1} V_{1} + C_{2} V_{2}}{C_{1} + C_{2}}$
Then the potential drop across $C_{1}$ is $\left(\right. V - V_{1} \left.\right)$ and $C_{2}$ is $\left(\right. V_{2} - V \left.\right)$ .
Charge stored on the capacitor of capacitance $C_{1}$ is
$q_{1}=C_{1}\left(\right. V - V_{1} \left.\right)$
Charge stored on the capacitor of capacitance $C_{2}$ is
$q_{2}=C_{2}\left(\right. V_{2} - V \left.\right)$
As $q_{1} = q_{2}$ [capacitors are in series]
$\therefore C_{1} \left(\right. V - V_{1} \left.\right) = C_{2} \left(\right. V_{2} - V \left.\right)$
$\Rightarrow V=\frac{C_{1} V_{1} + C_{2} V_{2}}{C_{1} + C_{2}}$