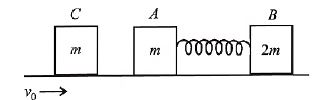
Q. Two bodies $A$ and $B$ of mass $m$ and $2m$ respectively are placed on a smooth floor. They are connected by a spring of negligible mass. A third body $C$ of mass m is placed on the floor. The body $C$ moves with a velocity $v_0$ along the line joining $A$ and $B$ and collides elastically with $A$. At a certain time after the collision it is found that the instantaneous velocities of $A$ and $B$ are same and the compression of the spring is $x_0$. The spring constant $k$ will be
AIEEEAIEEE 2012Work, Energy and Power
Solution:
Initial momentum of the system block $(C) = mv_0$. After striking with A, the block C comes to rest and now both block A and B moves with velocity v when compression in spring is $x_0$.
By the law of conservation of linear momentum
$mv_{0} = \left(m+2m\right)v \Rightarrow v = \frac{v_{0}}{3}$
By the law of conservation of energy K.E. of block C = K.E. of system + P.E. of system
$\frac{1}{2}mv^{2}_{0} = \frac{1}{2}\left(3m\right)\left(\frac{v_{0}}{3}\right)^{2}+\frac{1}{2}kx^{2}_{0}$
$\Rightarrow \quad \frac{1}{2}mv^{2}_{0} = \frac{1}{6} mv^{2}_{0} +\frac{1}{2}kx^{2}_{0}$
$\Rightarrow \quad \frac{1}{2}kx^{2}_{0} = \frac{1}{2}mv^{2}_{0} - \frac{1}{6}mv^{2}_{0} = \frac{mv^{2}_{0}}{3}$
$\therefore \quad k = \frac{2}{3}m\left(\frac{v_{0}}{x_{0}}\right)^{2}$