Q.
Two blocks with masses $m_{1}=3 \,kg$ and $m_{2}=5\, kg$ are connected by a light string that slides over a frictionless pulley as shown in figure. Initially, $m_{2}$, is held $5\, m$ off the floor while $m_{1}$ is on the floor. The system is then released. At what speed (in $m / s$ ) does $m_{2}$ hit the floor?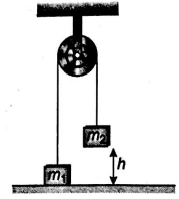
Work, Energy and Power
Solution:
