Question

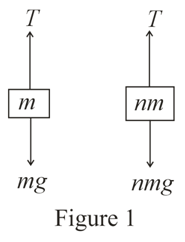
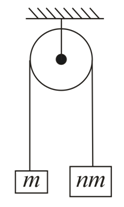
Two blocks of masses $m$ and $nm$ are connected by a massless string passing over a frictionless pulley. The value of $n$ for which both the blocks moves with an acceleration of $g/10$ is

• A. $9/11$
• B. $11/9$
• C. Both $\left(A\right)$ and $\left(B\right)$
• D. None

Answer 1

Answer: (C)

Case $\left(1\right)$ Assume that mass $m$ is accelerating upward.
$\therefore T-mg=\frac{m g}{10}\Rightarrow T=\frac{11 m g}{10}$
$\therefore nmg-T=\frac{n m g}{10}\Rightarrow nmg-\frac{11 m g}{10}=\frac{n m g}{10}$
$\frac{9}{10}n=\frac{11}{10}$ and $n=\frac{11}{9}$
Case $\left(2\right)$ Assume If $m$ mass is moving downward
$mg-T=\frac{m g}{10}\Rightarrow T=\frac{9 m g}{10}$
$\therefore T-nmg=nmg/10$
$\Rightarrow \frac{9}{10}mg-nmg=\frac{n m g}{10}$

$\frac{9}{10}=\frac{n}{10}+n=\frac{11 n}{10}$
$\therefore n=9/11$