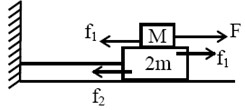
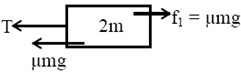
Q.
Two blocks of masses $m$ and $2m$ are placed one over the other as shown in the figure. The coefficient of friction between $m$ and $2m$ is $\mu $ and between $2m$ and ground is $\frac{\mu }{3}$ . If a horizontal force $F$ is applied on the upper block and $T$ is the tension developed in the string, then choose the incorrect alternative.
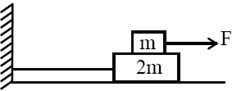
NTA AbhyasNTA Abhyas 2020Laws of Motion
Solution: