Q.
Two blocks, of masses $M$ and $2 M$, are connected to a light spring of spring constant $K$ that has one end fixed, as shown in figure. The horizontal surface and the pulley are frictionless. The blocks are released from rest when the spring is non-deformed. The string is light. Select the correct statement(s).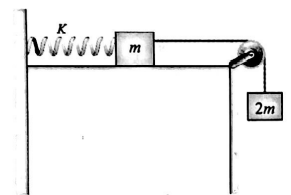
Work, Energy and Power
Solution: