Q.
Two blocks of equal mass are tied with a light string which passes over a massless pulley as shown in figure. The magnitude of acceleration of centre of mass of both the blocks is (neglect friction every where):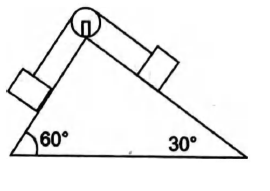
System of Particles and Rotational Motion
Solution:
