Q.
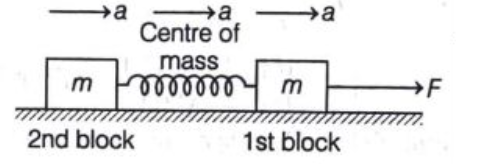
Two blocks of equal mass are connected with a massless spring of spring constant $2500 \,N / m ^{2}$ and length $10\, cm$ at rest on the frictionless horizontal plane. If a constant horizontal force $10\, N$ is applied as shown in the figure, find the maximum distance between the blocks.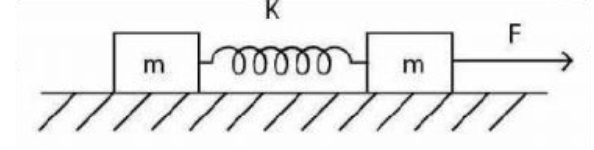
TS EAMCET 2020
Solution: