Question

Two blocks connected by a massless string slides down an inclined plane having an angle of inclination of $37^{\circ}$ The masses of the two blocks are $M_1=4\,kg$ and $M_2=2 \,kg$ respectively and the coefficients of friction of $M_1$ and $M_2$ with the inclined plane are $0.75$ and $0.25$ respectively. Assuming the string to be taut, find (a) the common acceleration of two masses and (b) the tension in the string. $(\sin 37^{\circ}=0.6, \cos 37^{\circ}=0.8)$.(Take $g=9.8\, m/s^2)$

Answer 1

Maximum force of friction between $M_1$ and inclined plane
$f_1=\mu M_1g \cos \theta= (0.75)(4)(9.8)(0.8)= 23.52 \,N$
$M_1 g \sin \theta=(4 )(9.8)(0.6) = 23.52\, N=F_1$ (say)
Maximum force of friction between $M_2$ and inclined plane
$f_2=\mu_2M_2g \cos \theta$
$= (0.25)(2)(9.8)(0.8)= 3.92 \,N$
$M_2g \sin \theta = (2)(9.8)(0.6)= 11.76 \,N=F_2$ (say)

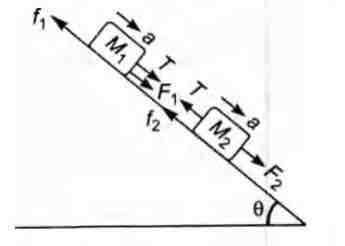
Both the blocks will be moving downwards with same acceleration $a$. Different forces acting on two blocks are as shown in above figure.
Equation of motion of $M_1$
$T+F_1-f_1=M_1a$
or $ T=4a ...(i)$
Equation of motion of $M_2$
$F_2 - T - f_2 = M_2a$
or $\, 7.84-T=2a \, ...(i)$
Solving Eqs. (i) and (ii), we get
$a = 1.3 \,m /s^2$ and $T = 5.2\,N$