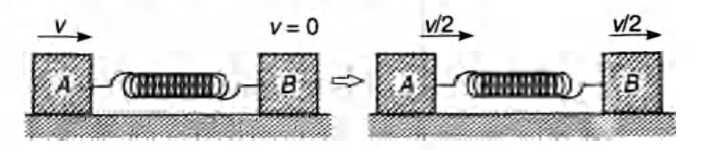
Q.
Two blocks $A$ and $B$ each of mass $m$, are connected by a massless spring of natural length Land spring constant $k$. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length, as shown in figure. $A$ third identical block $C$, also of mass m, moves on the floor with a speed $v$ along the line joining $A$ and $B$, and collides elastically with $A$. Then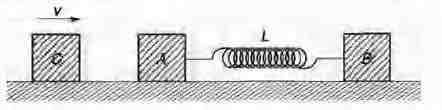
IIT JEEIIT JEE 1993System of Particles and Rotational Motion
Solution: