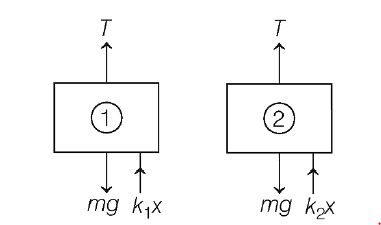
Question

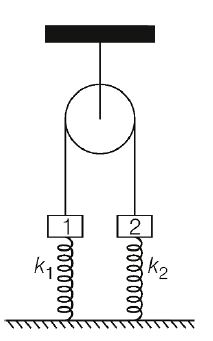
Two blocks $1$ and $2$ of equal mass $m$ are connected by an ideal string (see figure below) over a frictionless pulley. The blocks are attached to the ground by springs having spring constants $k_1$ and $k_{2}$ such that $k_{1} > k_{2}$. Initially, both springs are unstretched . Block $1$ is slowly pulled down a distance $x$ and released. Just after the re lease the possible values of the magnitudes of the accelerations of the blocks $a_{1}$ and a $a_{2}$ can be

• A. either $\left(a_{1}=a_{2}=\frac{\left(k_{1}+k_{2}\right)x}{2m}\right)$ or $(a_{1}=\frac{k_{1}x}{m}-g$ and $a_{2}=\frac{k_{2}x}{m}+g ) $
• B. $\left(a_{1}=a_{2}=\frac{\left(k_{1}+k_{2}\right)x}{2m}\right)$ only
• C. $\left(a_{1}=a_{2}=\frac{\left(k_{1}-k_{2}\right)x}{2m}\right)$ only
• D. either $\left(a_{1}=a_{2}=\frac{\left(k_{1}-k_{2}\right)x}{2m}\right)$ or $ \left(a_{1}=a_{2}=\frac{\left(k_{1}k_{2}\right)x}{\left(k_{1}+k_{2}\right)m}-g\right)$

Answer 1

Answer: (B)

Free body diagram for block $1$ and $2$ are as shown below.

So, equations of force balance are
$T+k_{1}x-mg=ma_{1}$
and $k_{2}x+mg -T=ma_{2}$
As string is in extensible,
$a_{1}=a_{2}=a $ (let)
Then adding both equations, we have
$\left(k_{1}+k_{2}\right)x=2ma$
$\Rightarrow a=\left(\frac{k_{1}+k_{2}}{2m}\right) .x$