Question

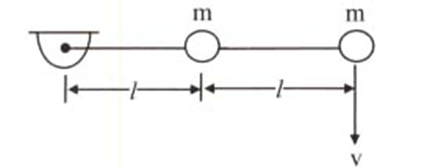
Two beads each of mass $m$ are fixed on a light rigid rod of length $2l$ which is free to rotate in a horizontal plane. The bead on the far end is given some velocity $v$ as shown in the figure. If $K_{cm}$ represents the kinetic energy of the centre of mass of the system and $K_{R}$ represents the rotational kinetic energy of the system, then what is the value of $\frac{K_{cm}}{K_{R}}$ ?

Answer 1

The distance of the centre of mass from the hinge,
$r_{cm}=\frac{m l + m \left(\right. 2 l \left.\right)}{m + m}=\frac{3}{2}l$
The angular velocity of the system,
$\omega =\frac{v}{2 l}$
The velocity of the centre of mass of the system,
$v_{cm}=\frac{3 l}{2}\omega =\frac{3}{4}v$
$\Rightarrow K_{cm}=\frac{1}{2}2mv^{2}_{cm}=\frac{9 m v^{2}}{16}$
The moment of inertia of the system about the hinge,
$I=ml^{2}+m\left(2 l\right)^{2}=5ml^{2}$
The rotational kinetic energy of the system,
$K_{\mathrm{R}}=\frac{1}{2} I \omega^2=\frac{1}{2} 5 m l^2\left(\frac{v}{2 l}\right)^2$
$\Rightarrow K_{R}=\frac{5 m v^{2}}{8}$
$\frac{K_{cm}}{K_{R}}=\frac{9 m v^{2}}{16}\times \frac{8}{5 m v^{2}}=0.9$