Question

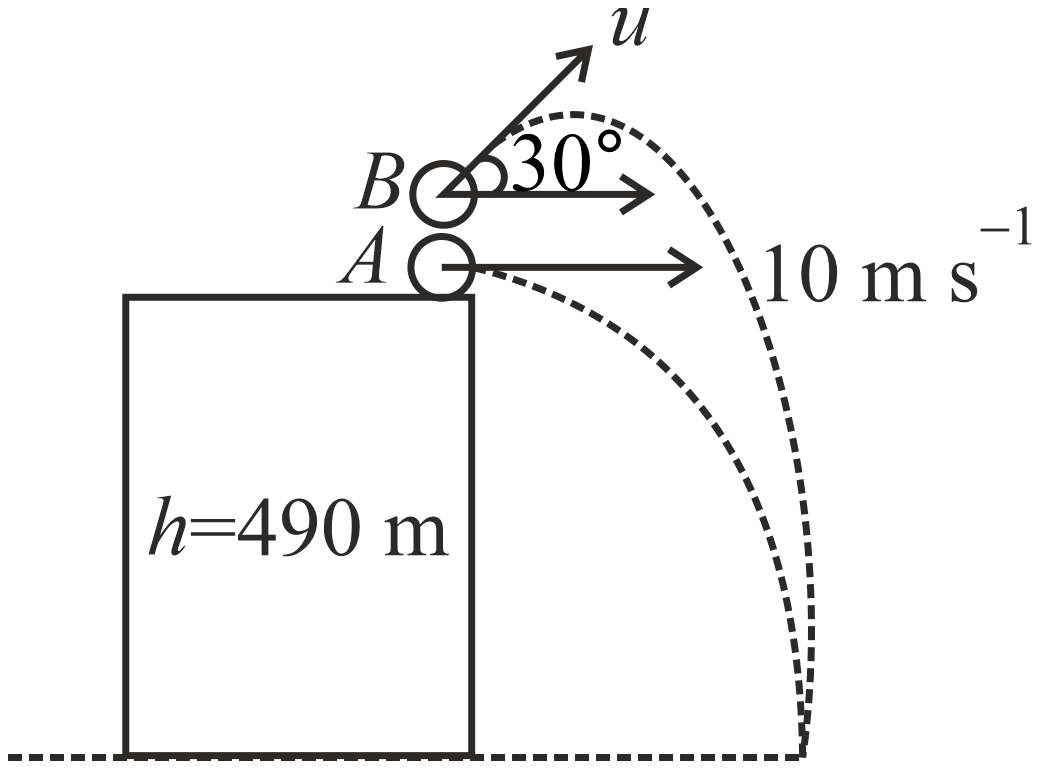
Two balls $A$ and $B$ are projected from the same height as shown in the figure. If the horizontal range of both the balls remains the same, then the speed $u$ of the second ball to the closest integer is $\ldots \ldots ms^{- 1}.$

Answer 1

The ball, $B$ , follows horizontal and angular projectile and the ball $A$ follows only horizontal projectile,
the height of the tower is, $h=490m$ , and both the particle follows the same range,
now for particle $A,$
$R=u\sqrt{\frac{2 h}{g}}=10\times \sqrt{\frac{2 \times 490}{9 . 8}}=100m$
and for oblique projectile,
$R=100m=ucos\theta \times t$
$\Rightarrow t=\frac{100}{u cos \left(\theta \right)}...\left(1\right)$
Now using it in vertical direction,
$\Rightarrow -490=usin\left(\theta \right)\times t-\frac{1}{2}gt^{2}$
$\Rightarrow -490=usin\left(30 ^\circ \right)\times \frac{100}{u cos \left(\theta \right)}-\frac{1}{2}g\left(\frac{100}{u cos \left(\theta \right)}\right)^{2}$
$\Rightarrow -490=usin\left(30 ^\circ \right)\times \frac{100}{u cos \left(30 ^\circ \right)}-\frac{1}{2}g\left(\frac{100}{u cos \left(30 ^\circ \right)}\right)^{2}$
$\Rightarrow -490=\frac{u}{2}\times \frac{2 \times 100}{u \sqrt{3}}-\frac{1}{2}\times 9.8\times \left(\frac{2 \times 100}{u \sqrt{3}}\right)^{2}$
$\Rightarrow -490=\frac{100}{\sqrt{3}}-\frac{196000}{u^{2} \times 3}$
$\Rightarrow \frac{196000}{u^{2} \times 3}=\frac{100}{\sqrt{3}}+490$
$\Rightarrow \frac{196000}{u^{2} \times 3}=\frac{100}{\sqrt{3}}+490$
$\Rightarrow u=10.9\approx11ms^{- 1}$