Question

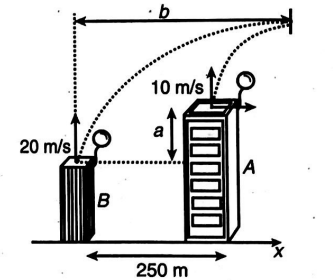
Two balloons are simultaneously released from two buildings $A$ and $B$. Balloon from $A$ rises with constant velocity of $10\, m\, s ^{-1}$, While the other one rises with constant velocity of $20\, m\, s ^{-1}$. Due to wind the balloons gather horizontal velocity $v_{x}=0.5\, y$, where $y$ is the height from the point of release. The buildings are at a distance of $250\, m$ and after some time $t$ the balloons collide. Find the difference in height (in $m$ ) of the buildings.

Answer 1

$20 \times t=10 t+a $
$\Rightarrow 10 t=a$
For $B:$
$v_{x}=\frac{y}{2} $
$\frac{d x}{d t}=\frac{20 t}{2} $
$\int\limits_{0}^{b} d x=\int\limits_{0}^{t} 10 t d t$
$b=5 t^{2}$.....(i)
For $A:$
$v_{x}=\frac{y}{2} $
$\frac{d x}{d t}=\frac{10 t}{2} $
$\int\limits_{250}^{b} d x=\int\limits_{0}^{t} 5 t d t $
$b-250=\frac{5 t^{2}}{2}$ ....(ii)
Using (i) and (ii), we get
$5 t^{2}-250=\frac{5 t^{2}}{2} $
$\Rightarrow t=10\, s $ and $ a=100 \,m$