Q.
Twelve wires of each of resistance $6$ ohms are connected to form a cube as shown in the figure. The current enters at a corner $A$ and leaves at the diagonally opposite corner $G$. The joint resistance across the corners $A$ and $G$ are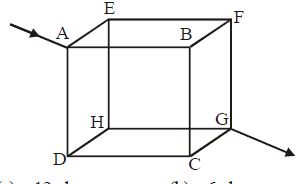
VITEEEVITEEE 2007
Solution:
