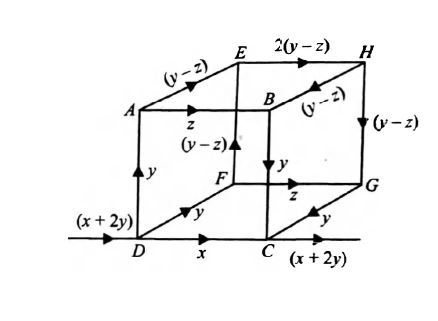
Question

Twelve wires, each of resistance $ 2 \Omega $ are connected to form a cube. Find the equivalent resistance between the adjacent corners of any face of the cube

• A. $ \frac{6}{7} \Omega $
• B. $ \frac{7}{6} \Omega $
• C. $ \frac{3}{4} \Omega $
• D. $ \frac{4}{3} \Omega $

Answer 1

Answer: (B)

From loops $FEHGF$ and $DCGFD$
$4y-5z=0$ and $x-2y-z=0$
$\therefore y={\frac{5}{14}}\,x$
If $R$ is the resistance between corners $C$ and $D$,
$(x+2y) R=xr$
$R=\left(\frac{x}{x+2y}\right)$
$r=\frac{xr}{\left(x+\frac{5}{7}x\right)}=\frac{7}{12}r $
Here, $r=2 \Omega$
$\Rightarrow R=\frac{7}{12}\times2$
$=\frac{7}{6} \Omega$