1. Tardigrade
  2. Question
  3. Mathematics
  4. To maximize the objective function z = 2x + 3y under the constraints x + y ≤ 30, x - y ≥ 0 , y ≤ 12, x ≤ 20 , y ≥ 3 and x ,y ≥ 0

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

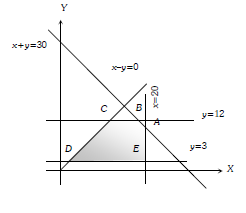
Q. To maximize the objective function $z = 2x + 3y $ under the constraints $x + y \leq 30, x - y \geq 0 , y \leq 12, x \leq 20 , y \geq 3$ and $x ,y \geq 0 $

Linear Programming

Solution:

The objective function is Max$z = 2x + 3y . $
The vertices are $A(20, 10), B(18 , 12) , C (12, 12) , D (3, 3)$ and E (20, 3). Hence the maximum value of the objective function will be at (18, 12).

Solution Image