Question

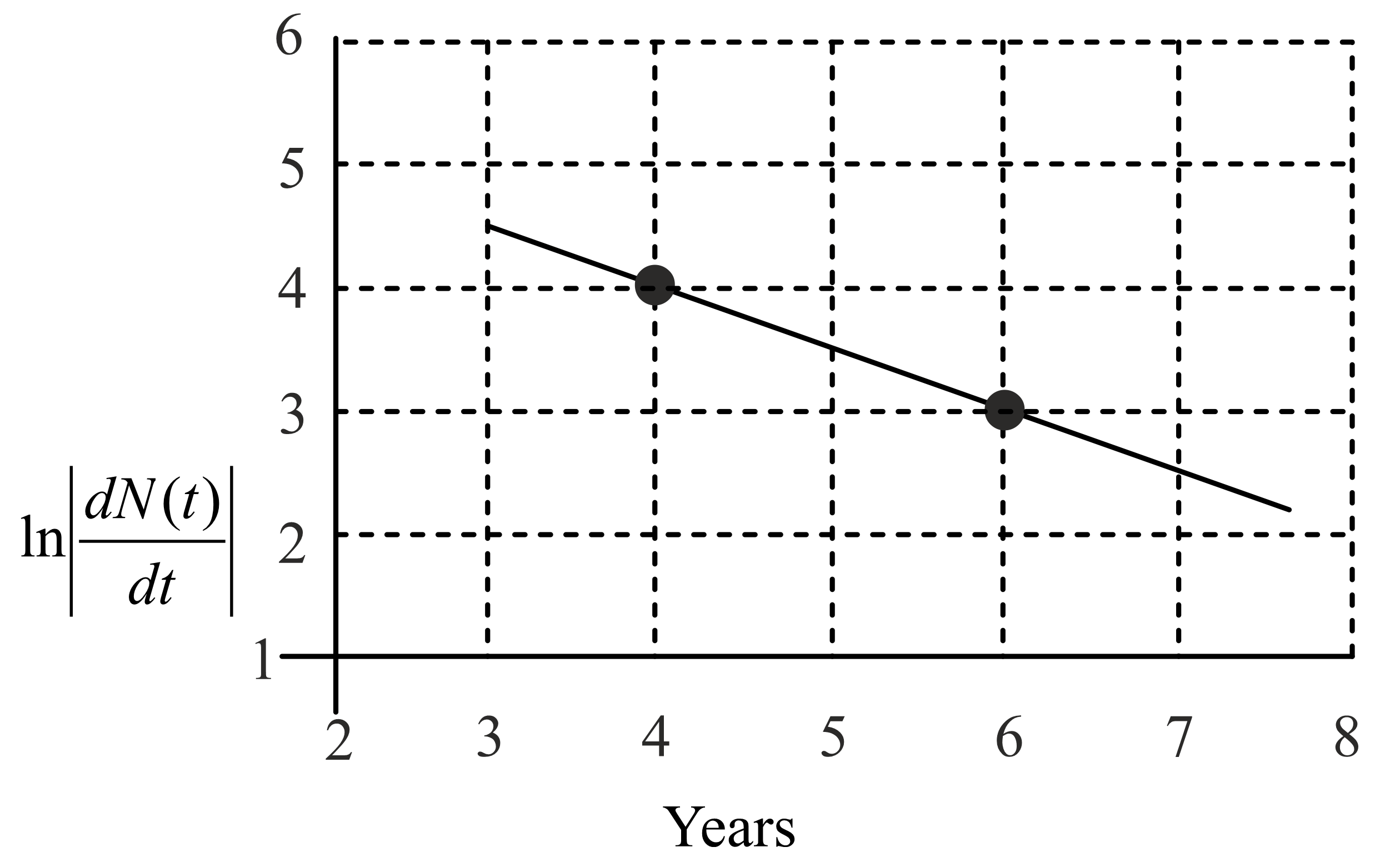
To determine the half life of a radioactive element, a student plots a graph of $\ln\frac{d N \left(\right. t \left.\right)}{d t}$ versus $t.$ Here, $\frac{d N \left(\right. t \left.\right)}{d t}$ is the rate of radioactive decay at time $t.$ If the number of radioactive nuclei of this element decreases by a factor of $p$ after $4.16$ years, the value of $p$ is:

Answer 1

According to radioactive decay law,
$N\left(t\right)=N_{0}e^{- \lambda t}\Rightarrow \left|\frac{d N}{d t}\right|=N_{0}\lambda e^{- \lambda t}$
Taking $log$ both sides,
$\ln\left|\frac{d N}{d t}\right|=\left[\ln \left(N_{0} \lambda \right)\right]-\lambda t$
This is a straight line equation with slope $m=-\lambda $
From the given graph,
$m=\frac{4 - 3}{4 - 6}=-0.5$
$\Rightarrow \lambda =0.5\,yr^{- 1}$
$t_{1 / 2}=\frac{0 . 693}{\lambda }=\frac{0 . 693}{0 . 5}=1.386\,yr$
Let the number of half life $=n$
$4.16=nt_{1 / 2}\Rightarrow n=3$
So, $p=2^{n}=2^{3}=8$