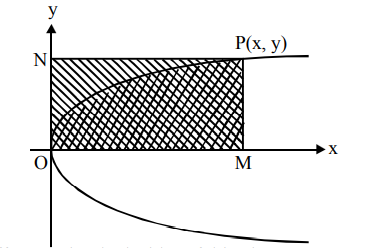
Question

Through any point $(x, y)$ of a curve which passes through the origin, lines are drawn parallel to the co-ordinate axes. The curve, given that it divides the rectangle formed by the two lines and the axes into two areas, one of which is twice the other, represents a family of

• A. circles
• B. pair of straight lines
• C. parabolas
• D. rectangular hyperbolas

Answer 1

Answer: (C)

Let $P(x, y)$ be the point on the curve passing through the origin $O(0,0)$ and let $P N$ and $P M$ be the lines parallel to the $x$ -and $y$ -axis, respectively. If the equation of the curve is
$y=y(x)$, the area $P O M$ equals
$\int\limits_{0}^{x} y d x$ and the area $PON$
equals $x y-\int\limits_{0}^{x} y d x .$
Assuming that $2(P O M)=P O N$, we therefore have
$2 \int\limits_{0}^{x} y d x=x y-\int_{0}^{x} y d x$
$ \Rightarrow 3 \int\limits_{0}^{x} y d x=x y$

Differentiating both sides of this gives
$3 y=x \frac{d y}{d x}+y $
$\Rightarrow 2 y=x \frac{d y}{d x} $
$\Rightarrow \frac{d y}{y}=2 \frac{d x}{x}$
$\Rightarrow \log y=2 \log x+C $
$\Rightarrow y=C x^{2}$
With $C$ being a constant. This solution represents a parabola. We will get a similar result if we have started instead with $2(P O N)=P O M$