Q.
Three uniform thin aluminum rods each of length $2\, m$ form an equilateral triangle $P Q R$ as shown in the figure. The mid point of the rod $P Q$ is at the origin of the coordinate system. If the temperature of the system of rods increases by $50^{\circ} C$, the increase in $y$ -coordinate of the centre of mass of the system of the rods is ............ $mm$. (Coefficient of volume expansion of aluminium $=12 \sqrt{3} \times 10^{-6} K ^{-1}$ )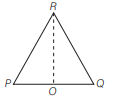
AP EAMCETAP EAMCET 2017
Solution:
