Question

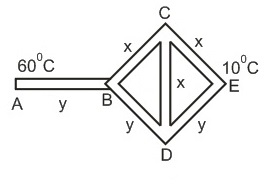
Three rods of material $x$ and three rods of material $y$ of identical length and cross sectional area are connected as shown in the figure. If the end $A$ is maintained at $60^{\circ} C$ and the junction $E$ at $10^{\circ} C$, then the temperature of junction $C$ is [Given the thermal conductivity of $x$ is $0.92\, W / m . K$ and that of $y$ is $0.46 \,W / m . K$ ]

• A. $10^{\circ} C$
• B. $20^{\circ} C$
• C. $30^{\circ} C$
• D. $40^{\circ} C$

Answer 1

Answer: (B)

Treating the given network of rods in terms of thermal resistance $R_{x}$ and $R_{y}$ with
$R _{ x }=\frac{ L }{ A \times 0.92}$ and $R _{ y }=\frac{ L }{ A \times 0.46}\left[\right.$ as $\left.R =\frac{ L }{ AK }\right]$
so that if $R _{ x }= R , R _{ y }=2 R _{ x }=2 R$
Now as in this bridge $[(P / Q)=(R / S)]$, so the bridge is balanced, i.e., the temperature at junctions $C$ and $D$ is equal and the rod CD becomes ineffective as no heat will flow through it.
Now as the thermal resistance of the bridge between junctions $B$ and $E$ is $\frac{1}{( R )_{ nE }}=\frac{1}{( R + R )}+\frac{1}{(2 R +2 R )}$, i.e., $( R )_{ BE }=\frac{4}{3} R$
The total resistance of bridge between $A$ and $E$ will be
$R_{\text {eq }}=R_{A B}+R_{B E}=2 R+(4 / 3) R=(10 / 3) R$
So the net rate of flow of heat through the bridge will be
Now if $T_{B}$ is the temperature at $B$,
But $\left[\frac{ dQ }{ dt }\right]_{ AB }=\frac{ dQ }{ dt }$,i.e., $\frac{60- T _{ B }}{2 R }=\frac{15}{ R }$,i.e., $T _{ B }=30^{\circ} C$
Also at $B$
$\left[\frac{ dQ }{ dt }\right]_{ AB }=\left[\frac{ dQ }{ dt }\right]_{ BC }+\left[\frac{ dQ }{ dt }\right]_{ BD }$
i.e. $\frac{15}{ R }=\frac{30- T _{ C }}{ R }+\frac{30- T _{ D }}{2 R }$
and as $T_{C}=T_{D}=T, 30=3(30-T)$,
i.e., $T_{C}=T_{D}=T=20^{\circ} C$