Q.
Three rods of material $x$ and three rods of material $y$
are connected as shown in figure. All are identical in length and cross sectional area. If end $A$ is maintained at $60^{\circ} C$, end $E$ at $10^{\circ} C$, thermal conductivity of $x$ is $0.92 cal s ^{-1} cm ^{-1 \circ} C ^{-1}$ and that of $y$ is $0.46 cal s ^{-1} cm ^{-1}{ }^{\circ} C ^{-1}$
then find the temperatures of junctions $B, C, D .$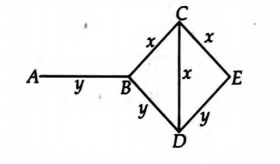
Thermal Properties of Matter
Solution:
