Q.
Three rods of equal length $l$ are joined to form an equilateral triangle $PQR. O$ is the mid point of $PQ$. Distance $OR$ remains same for small change in temperature.
Coefficient of linear expansion for $PR$ and $RQ$ is same i.e. $\alpha_2$ but that for $PQ$ is $\alpha_1$. Then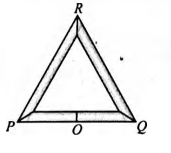
Thermal Properties of Matter
Solution: