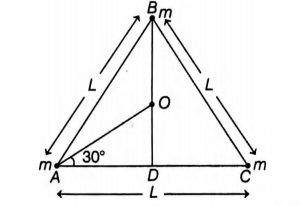
Question

Three point masses each of mass ' $m$ ' are kept at the corners of an equilateral triangle of side 'L. The system rotates about the center of the triangle without any change in the separation of masses during rotation. The period of rotation is directly proportional to $\left(\cos 30^{\circ}=\sin 60^{\circ}=\frac{\sqrt{3}}{2}\right)$

• A. $\sqrt{L}$
• B. $L^{3 / 2}$
• C. $L$
• D. $L^2$

Answer 1

Answer: (D)

The situation can be shown below,

where, $O$ is the centroid of equivalent triangle. The length $A O$ can be found by
$AO = \sqrt{OD^2 + AD^2}$
$= \sqrt{(\frac{1}{3} BD)^2 + AD^2} = \sqrt{\frac{1}{9} \times \left(\frac{\sqrt{3}}{2} L\right)^2 + \frac{L^2}{4}}$
$ = \sqrt{\frac{1}{12} L^2 + \frac{L^2}{4} } = \frac{L}{\sqrt{3}}$
The moment of inertia about $O$ is given by
$I = MR^2$
$= m \times \left(\frac{L}{\sqrt{3}}\right)^2 = \frac{mL^2}{3} \dots$(i)
According to law of conservation of angular momentum,
$I \omega =$ constant
$I \times \frac{2\pi}{T} = $ Constant
$\Rightarrow T \propto I$
From Eq. (i), we get
$T \propto L^2$