Question

Three point charges q, 2q and 8q are to be placed on a 9 cm
long straight line. Find the positions where the charges
should be placed such that the potential energy of this system
is minimum. in this situation, what is the electric field at the
position of the charge q due to the other two charges ?

Answer 1

For potential energy to be minimum the bigger charges
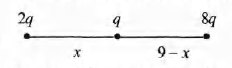
should be farthest. Let x be the distance of q from 2q. Then
potential energy of the system shown in figure would be
$ U=K\bigg[\frac{(2q) (q)}{x}+\frac{(8q) (q)}{(9-x)}+\frac{(2q) (8q)}{9}\bigg]$
Here $ \, \, K=\frac{1}{4\pi\varepsilon_0}$
For U to be minimum $\frac{2}{x}+\frac{8}{9-x}$ should be minimum.
$\frac{d}{dx}\bigg[\frac{2}{x}+\frac{8}{9-x}\bigg]=0$
$\therefore \frac{-2}{x}+\frac{8}{(9-x)^2}=0$
$\therefore \frac{x}{9-x}=\frac{1}{2}$
or $ x = 3\, cm$
i.e. distance of charge q from 2q should be 3 cm.
Electric field at q
$ E=\frac{K(2q)}{(3 \times 10^{-2})^2}-\frac{K(8q)}{(6 \times 10^{-2})^2}=0$