Q.
Three point charges of $3 \,\mu C\,, 4 \,\mu C$, and $5 \,\mu C$
are arranged at the three corners of a right angled triangle $A B C$ as shown in the figure. The work done in moving the charges at $A$ and $C$, so that the three charges are located at the three corners of an equilateral triangle of side $3 \,cm$ is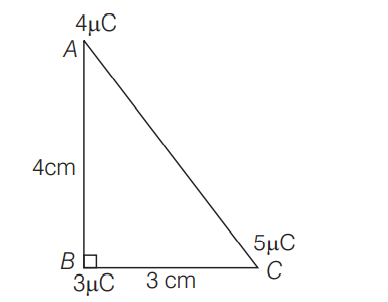
AP EAMCETAP EAMCET 2019
Solution:

