Question

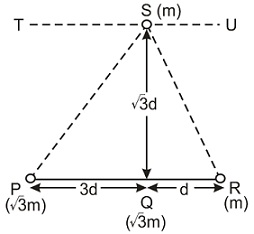
Three particles $P$ , $Q$ and $R$ are placed on a straight line as shown in the figure. The masses of $P$ , $Q$ and $R$ are $\sqrt{3} m$ , $\sqrt{3} m$ and $m$ respectively. The gravitational force on a fourth particle $S$ of mass $m$ is equal to

• A. $\frac{\sqrt{3} Gm^{2}}{2 \textit{d}^{2}}$ in ST direction only
• B. $\frac{\sqrt{3} Gm^{2}}{2 \textit{d}^{2}}$ in SQ direction and $\frac{\sqrt{3} Gm^{2}}{2 \textit{d}^{2}}$ in SU direction
• C. $\frac{\sqrt{3} Gm^{2}}{2 \textit{d}^{2}}$ in SQ direction only
• D. $\frac{\sqrt{3} Gm^{2}}{2 \textit{d}^{2}}$ in SQ direction and $\frac{\sqrt{3} Gm^{2}}{2 \textit{d}^{2}}$ in ST direction

Answer 1

Answer: (C)

Along the direction parallel to TU
Net force $= \frac{\textit{G} \sqrt{3} mm}{1 2 d^{2}} cos \text{30}^{^\circ } - \frac{\textit{Gm}^{2}}{4 d^{2}} cos \text{60}^{^\circ }$
$= \frac{\textit{Gm}^{2}}{8 \textit{d}^{2}} - \frac{\textit{Gm}^{2}}{8 \textit{d}^{2}} = 0$
Along the direction perpendicular to TU
Net force $= \frac{\textit{G} \sqrt{3} m^{2}}{1 2 d^{2}} cos \text{60}^{^\circ } + \frac{\textit{G} \sqrt{3} m^{2}}{3 d^{2}} + \frac{\textit{Gm}^{2}}{4 d^{2}} cos \text{30}^{^\circ }$
$= \frac{\sqrt{3} Gm^{2}}{2 4 d^{2}} + \frac{\sqrt{3} Gm^{2}}{3 d^{2}} + \frac{\sqrt{3} Gm^{2}}{8 d^{2}}$
$= \frac{\sqrt{3} Gm^{2}}{\textit{d}^{2}} \left[\frac{1 + 8 + 3}{2 4}\right] = \frac{\sqrt{3} Gm^{2}}{2 d^{2}} \text{along SQ}$