Question

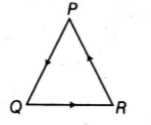
Three particles $ P, Q $ and $ R $ are at rest at the vertices of an equilateral triangle of side $ s $ . Each of the particles starts moving with constant speed $ v \,ms^{-1}. P $ is moving along $ PQ, Q $ along $ QR $ and $ R $ along $ RP $ . The particles will meet each other at time $ t $ given by

• A. $ \frac{s}{v} $
• B. $ \frac{3s}{v} $
• C. $ \frac{3s}{2v} $
• D. $ \frac{2s}{3v} $

Answer 1

Answer: (D)

The velocity component towards centroid $O$ of
triangle $= v \cos \,\theta$
$ = v \, \cos \,30^{\circ} = \frac{\sqrt{3}}{2} v$
Distance $ P O = - \frac{2}{3}$ of altitude
$ = \frac{2}{3} \times \frac{\sqrt{3}}{2} s = \frac{1}{\sqrt{3}} s$
$\Rightarrow $ Time $ = \frac {\text{Distance}}{\text{Speed}}$
$ = \frac{\frac{1}{\sqrt{3}} s}{\frac{\sqrt{3}}{2} v} $
$= \frac{2}{3} \cdot \frac{s}{v} $