Q.
Three particles, each of mass $m$ grams situated at the vertices of an equilateral triangle $ABC $ of side $l\, cm$ (as shown in the figure). The moment of inertia of the system about a line $AX$ perpendicular to $AB$ and in the plane of $ABC$, in gram $ -c{{m}^{2}} $ units will be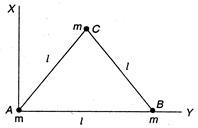
ManipalManipal 2007
Solution:

