Question

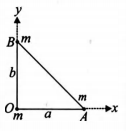
Three particles, each of mass $m$ are placed at the corners of a right angled triangle as shown in figure. If $O A=a$ and $O B=b,$ the position vector of the centre of mass is (Here $\hat{i}$ and $\hat{j}$ are unit vectors along $x$ and $y$ axes respectively).

• A. $\frac{1}{3}(a \hat{i}+b \hat{j})$
• B. $\frac{1}{3}(a \hat{i}-b \hat{j})$
• C. $\frac{2}{3}(a \hat{i}+b \hat{j})$
• D. $\frac{2}{3}(a \hat{i}-b \hat{j})$

Answer 1

Answer: (A)

The $(x, y)$ co-ordinates of the masses at $O, A$ and $B$
respectively are (refer to figure as given in the question)
$\left(x_{1}=0, y_{1}=0\right),\left(x_{2}=a, y_{2}=0\right)$ and $\left(x_{3}=0, y_{3}=b\right)$
The $(x, y)$ co-ordinates of the centre of mass are
$X_{ CM }=\frac{m_{1} x_{1}+m_{2} x_{2}+m_{3} x_{3}}{m_{1}+m_{2}+m_{3}}=\frac{m \times 0+m \times a+m \times 0}{m+m+m}=\frac{a}{3}$
$Y_{ CM }=\frac{m_{1} y_{1}+m_{2} y_{2}+m_{3} y_{3}}{m_{1}+m_{2}+m_{3}}=\frac{m \times 0+m \times 0+m \times b}{m+m+m}=\frac{b}{3}$
The position vector of the centre of mass is
$\vec{R}_{ CM }=X_{ CM } \hat{i}+Y_{ CM } \hat{j}=\frac{a}{3} \hat{i}+\frac{b}{3} \hat{j}=\frac{1}{3}(a \hat{i}+b \hat{j})$