Q.
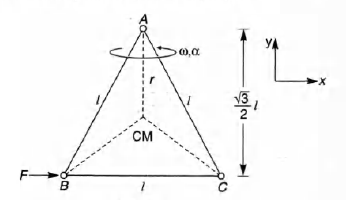
Three particles A , B and C, each of mass m, are connected to each other by three massless rigid rods to form a rigid , equilateral triangular body of side l. This body is placed on a horizontal frictionless table (x-y plane) and is hinged to it at the point A, so that it can move without friction about the vertical axis through A (see figure). The body is set into rotational motion on the table about/! with a constant angular velocity $\omega$.
(a) Find the magnitude of the horizontal force exerted by the hinge on the body.
(b) At time T, when the side BC is parallel to the x-axis, a force F is applied on B along BC (as shown). Obtain the x-component and the _y-component of the force exerted by the hinge on the body, immediately after time T.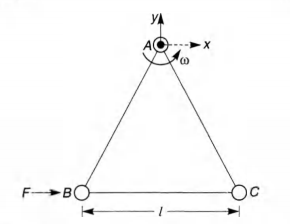
IIT JEEIIT JEE 2005System of Particles and Rotational Motion
Solution:
(a) The distance of centre of mass (CM) of the system about point A will be
$r=\frac{l}{\sqrt3}$
Therefore, the magnitude of horizontal force exerted by the hinge on the body is
F = centripetal force or $F=(3m)r\omega^2$
or $F=(3m)\bigg(\frac{l}{\sqrt3}\bigg)\omega^2$ or $F=\sqrt3 ml\omega^2$
(b) Angular acceleration of system about point A is
$\alpha=\frac{\tau_A}{I_A}=\frac{(F)\bigg(\frac{\sqrt3}{2}l\bigg)}{2ml^2}=\frac{\sqrt3F}{4ml}$
Now, acceleration of CM along x-axis is
$a_x=r\alpha=\bigg(\frac{1}{\sqrt3}\bigg)\bigg(\frac{\sqrt3F}{4ml}\bigg)$ or $a_x=\frac{F}{4m}$
Let $F_x$ be the force applied by the hinge along x-axis.
Then, $F_x+F=(3m)a_x$
or $F_x+F=(3m)\bigg(\frac{F}{4m}\bigg)$
or $F_x+F=\frac{3}{4}F$
Further if $F_y$ be the force applied by the hinge along y-axis. Then,
$F_y$ = centripetal force
or $F_y=\sqrt3 ml\omega^2$